深入理解数据库系统(三):数据库设计
本篇将介绍数据库设计相关的概念。主要分为两个部分:数据库概念模型设计和关系型数据库设计。它们分别对应的设计方法是 E-R 模型(Entity-Relationship Model)和标准化(Normalization)。
数据库设计和 E-R 模型
数据库设计过程
设计过程
- 需求分析阶段。与用户和领域专家交流,收集需求,充分地描述出预期的数据库用户需要的数据。这个阶段产出的是用户需求的规范。
- 概念设计阶段。选择一个数据模型,将用户需求转换为数据库概念模式。这个阶段主要是专注于描述数据和数据之间的关系。用专业的、概念的数据模型去描述数据结构,主要使用 entity-relationship model 和 normalization 方式去设计。这个阶段一般产出的是实体关系图(E-R图)。完整的概念设计 schema 还包含功能需求规范。描述用户对数据的操作类型,如修改,查询和取出具体的数据,删除数据。
- 逻辑设计阶段。将抽象的数据模型转换为数据库的实现。将概念模型转换为数据库系统使用的模型,如将 entity-relationship model 转换为 relational model。
- 物理设计阶段。设计物理存储的细节。包括文件组织的形式和选择索引结构。
物理的 schema 相对来说是比较容易改变的,而改变逻辑的 schema 是很难的,可能会影响到大量分散在应用程序中的查询和更新代码。因此,在构建应用程序之前,必须谨慎地和考虑周全地进行数据库设计。
设计中常见的问题
- 冗余(Redundancy)。冗余的信息表示可能导致重复的信息出现不一致。如一些过时的或错误的信息依然存在数据库中。信息应该准确的出现在一个地方。
- 不完全(Incompleteness)。一个坏的设计可能会使企业的某些方面难以建模或无法建模。不合理的分解关系的属性,导致难以插入一个新增的数据,或者必须其它属性设为 null。如,没有单独的课程表,只有课程设置表,当新增课程时,无法插入课程属性到课程设置表。
E-R 模型
E-R 模型可以将现实世界中企业的含义和相互作用映射到一个概念的模式。E-R 数据模型采用三个基本的概念:实体集,关系集,和属性。
Entity Sets
实体(Entity)是现实中的一个事情或一个对象,每个对象是与其它对象有区别的。如大学中的一个人就是一个实体。一个实体有一组属性,它的属性值可以唯一标识一个实体。如,一个人可能有一个身份证号码属性,这个属性值可以唯一的标识一个人。一个实体可以是具体的,如一个人或一本书等,也可以是抽象的,如一个课程或一个机票预订等。
实体集(Entity Set)是一组有相同类型的实体,它们共享相同的属性。
Relationship Sets
关系(Relationship)是几个实体之间的关联。如一个老师实体和一个学生实体之间有一个指导的关系。
关系集(Relationship Sets)是一组相同类型的关系。多个实体集之间的关系总和构成了关系集。实体集之间的关联称为参与,如 实体集 E1,E2… 参与关系集 R。实体在关系中扮演的功能称为该实体的角色。
相同的实体集之间的可能超过一个关系集。两个实体集之间的称为二元关系集(Binary Relationship Set)。然而,关系集可能涉及超过两个实体集。参与一个关系集的实体集的数量称为Degree of the relationship set。二元关系集的 degree 是 2,三元关系集的 degree 是 3。
Attributes
每一个属性有一组允许的值,称为 domain 或者 value set。每一个实体可以用一组属性和属性值对来描述。
E-R 模型中的属性类型有:
- 简单(Simple)和组合(Composite)属性。组合属性可以分为多个子部分,如 name 属性可以由 first_name, middle_name, 和 last_name 组合而成。
- 单值(Single-valued)和 多值(Multivalued)属性。单值属性表示只能出现一个值,如 ID 属性只能一个,多值属性表示可以有多个值,如 phone_number 可以有多个电话号码。
- 派生属性(Derived)。这类属性的值可以从其它相关属性的值得出。如 age 可以从 date_of_birth 属性值得出。
一个属性为 null 值表示不存在或者未知。
Constraints
E-R 模型中主要有两种约束:映射基数和参与约束。
映射基数(Mapping Cardinality)主要用于描述二元关系集。映射基数的类型有:
- One-to-one。一个实体 A 最多关联一个实体 B。
- One-to-many。一个实体 A 可以关联多个实体 B。
- Many-to-one。多个实体 A 可以关联一个实体 B。
- Many-to-many。一个实体 A 可以关联多个实体 B。一个实体 B 也可以关联多个实体 A。
参与约束(Participation Constraints)表示一个实体集参与一个关系的数量。主要有两种参与约束:
- Total。它表示一个实体集所有实体都参与了一个关系集。
- Partial。它表示一个实体集部分实体参与了一个关系集。
Keys
一个 key (键)是能够区分不同的实体的一组属性。Superkey 表示可以区分实体的一组属性。Candidate key 表示最小的 Superkey 即用来区分实体的最小的属性集。Primary key 与 candidate key 是相同的,只是在不同的地方的表述,Primary key 用在数据库的表述中,而另一个用在 E-R 模型中。
去除冗余的属性
设计一个数据库的 E-R 模型,通常是先确定有哪些实体集,为实体集选择合适的属性,为实体集建立合适的关系。一些属性同时出现在多个实体集中,为它们建立关系集,并取出重复的属性。
E-R 图
E-R 图可以图形化地表示数据库地总体的逻辑结构。E-R 图简单而清晰,被广泛使用在 E-R 模型中。
基本结构
E-R 图主要的组件有:
分为两部分的长方形(Rectangle Divided):用来表示实体集。
菱形(Diamond):表示关系集。
没有划分的长方形(Undivided Rectangle):表示一个关系集的属性。
线(Line):用来连接实体集和关系集。
虚线(Dashed Line):用来连接一个关系集的属性到另一个关系集。
双线(Double Line):用来指出一个实体集完全参与一个关系集。即表示参与约束。
双线菱形(Double Diamond):表示关系集是被弱实体连接的。
实体集的主键属性用下划线标识。
一个简单的 E-R 图,如下所示:
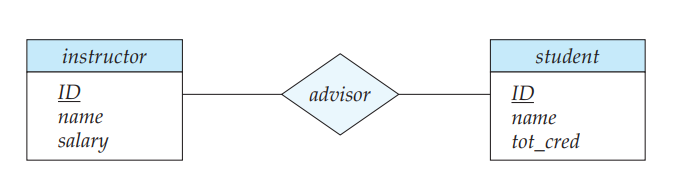
E-R 图映射基数的表示
E-R 图使用关系集到实体集之间的有向线(Directed Line)和无向线(Undirected Line)来表示 one-to-one,one-to-many 等映射基数。有向线表示 one,无向线表示 many。如下 E-R 图表示 student 与 instructor 的 many-to-one 关系。
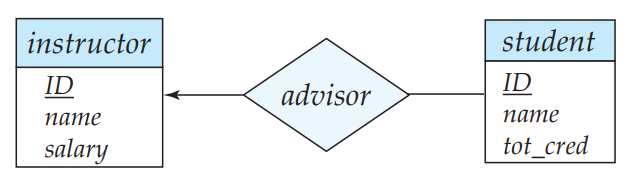
更复杂的映射基数使用 l..h 表示,l 表示最小的基数,h 表示最大的基数。基数的值可以是 0 到无穷, * 表示无穷。常见的表示,如 1..1,0..* 。左边线上的基数表示右边实体集的参与数量,反之亦然。
弱实体集
一个实体集没有足够的属性去组成一个主键,即没有主键的实体集称为弱实体集(Week Entity Sets)。一个实体必须依赖另一个实体的属性才能完整,即实体需要添加其它实体的属性才能被唯一标识或者说能实现主键。
为了使弱实体集有意义,它必须关联另一个实体集,称为标识实体集(Identifying Entity Set)或所有者实体集(owner entity set)。每个弱实体必须与一个标识实体相关联; 就是说,弱实体集依赖于标识实体集而存在。 标识实体集拥有它标识的弱实体集。 将弱实体集与标识实体集相关联的关系称为标识关系(Identifying Relationship)。如 section(课时) 必须依赖 course (课程)的 cource_id。
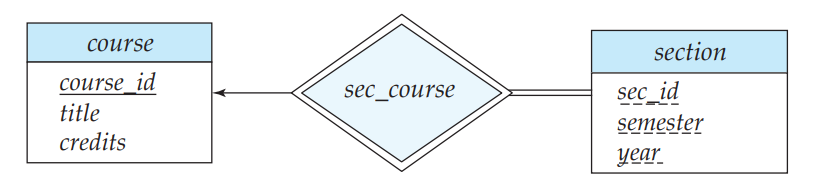
更多的 E-R 图的表示,如:
组合属性(Composite Attributes)
角色(Role)
非二元关系集(Nonbinary Relationship Sets)
这些 E-R 表示的内容,不详细解释了,如有兴趣可查阅文章最后给出的参考书籍。
一个大学的 E-R 图例子如下图所示:
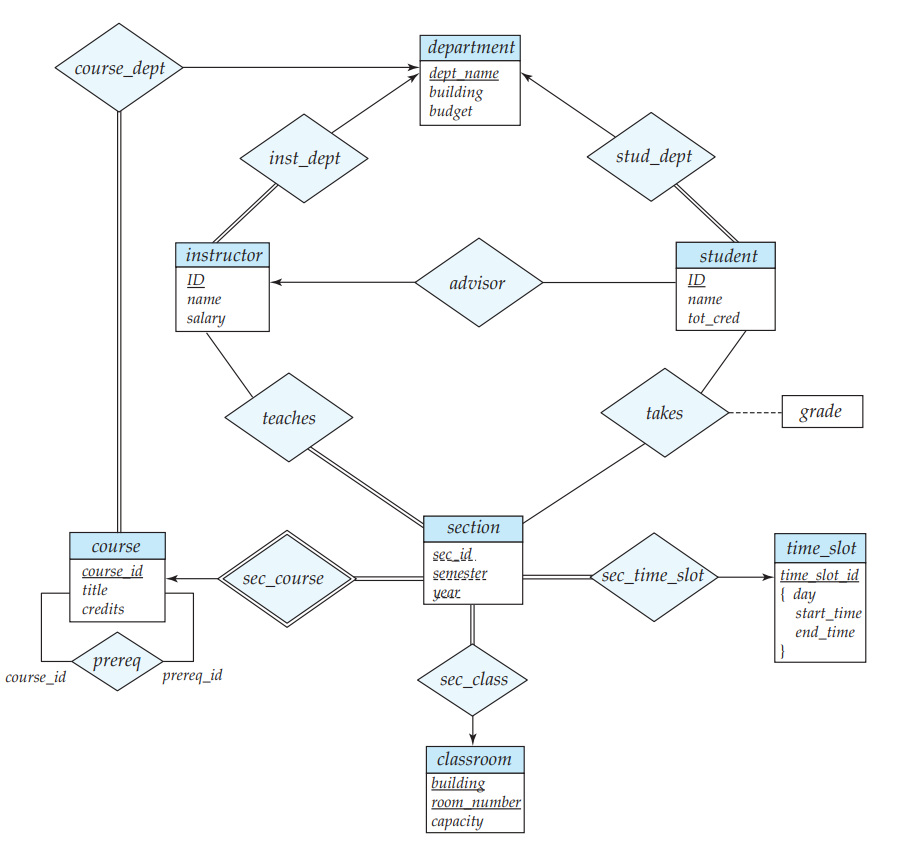
E-R 模型转换为关系模型
E-R 模型和关系模型都是抽象的逻辑的表示真实世界。要实现数据库必须把 E-R 模型转换为数据库系统对应的数据模型。当前小节,我们描述如何将 E-R 模型转换为关系型数据库的关系模型。主要涉及两个问题:E-R schema 如何转换为 relation schema,E-R schema 中的约束如何转换为 relation schema 的约束。
强实体集的简单属性的表示
E-R 模型中的一个 Entity Set 的每个属性对应一个 Relation 的每个元组。
强实体集的复杂属性的表示
组合属性(Composite Attributes)。组合属性中的每一个属性作为一个单独的属性。
多值属性(Multivalued Attributes)。为多值属性单独创建一个表。如一个教师有多个手机号码,可以单独创建一个表 instructor_phone (ID, phone number)。
派生属性(Derived Attributes)。派生是属性可以简单的作为表的属性。
弱实体集的表示
把依赖的实体集的属性与当前表属性组合成主键,同时为依赖的属性创建一个外键约束。
关系集的表示
many-to-many。组合所有参与实体集的主键作为关系集的主键。
one-to-one。任意选一个实体集的主键作为关系集的主键。
many-to-one or one-to-many。选择 many 那一边的实体集的主键作为关系集的主键。
n-ary without any arrows edges。组合所有参与实体集的主键作为关系集的主键。
n-ary with an arrow edge。组合所有不在箭头那边的实体集的主键作为关系集的主键。
Schema 的冗余
连接弱实体集和强实体集的关系集的 schema 是多余的。E-R 图中的这一类关系集不需要出现在数据库关系型模型中。
Schema 的结合
Schema 的结合表示:去除关系集,使它结合到实体集中。常见的结合如下:
one-to-one 中的关系集,可以结合在任一实体集的 schema 中。
many-to-one or one-to-many 的关系集,可以结合在 many 那边的实体集的 schema 中。
many-to-many 的关系集一般无法与实体集结合。
去除了关系集,一个实体集使用外键关联另一个实体集。
不完全参与关系结合后的实体集,可以使用 null 表示不存在的关联。
E-R 模型设计中的问题
有时实体集和关系集是不明确的,可能有大量不同的方式定义实体集和关系集。我们讨论一些基本的 E-R 模型设计的问题。
Entity Sets versus Attributes
一个实体有多值属性,这个多值属性是设计为一个属性还是一个实体集?
这需要看具体情况,如 instructor 实体集有一个多值属性 phone_number。如果这个多值属性的每个属性值需要维护额外的信息,如一个手机号码需要指定一个地点属性。这种情况下,多值属性需要设计成一个实体集 inst_phone(phone_number, location), inst_phone 实体集与 instructor 实体集建立一个关系集。
Entity Sets versus Relationship Sets
一个对象应该表示为实体集还是关系集,有时候它是不明确的。
如学生(student)实体集和课时(section)实体集之间的对象应该如何表示?可以表示为一个关系 take。也可以表示为 一个实体登记(registration) 和两个关系 section_reg 和 student_reg。
一个对象是使用关系集还是实体集一个重要的参考准则:关系集是实体集之间的动作。
Binary versus n-ary Relationship Sets
当存在多元关系集时,多元关系集应该使用二元关系集代替。
Placement of Relationship Attributes
关系集的属性在结合的实体集中。如 instructor 和 student 之间是 one-to-many 的关系,其中关系集 advisor 有一个属性 date 表示成为一个学生的指导者的日期。在结合的时候这个属性可以放在 student 实体集中。
扩展的 E-R 特性
Specialization
实体集包含实体子集,这些子集在某种程度上不同于集合中的其它实体。
设计子集实体集的过程称为 Specialization。一个例子如下图所示:
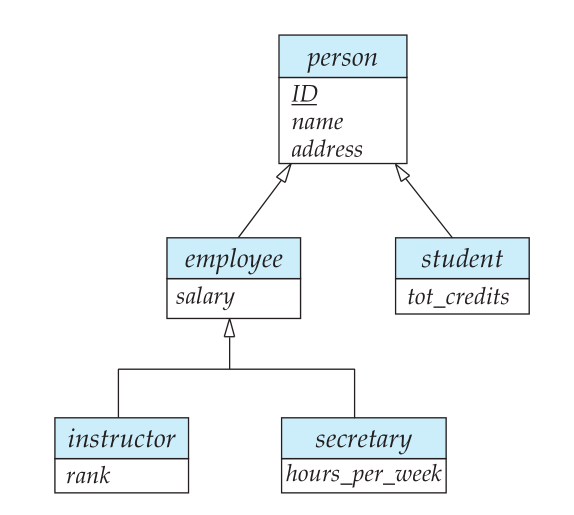
Generalization
Generalization 是 specialization 的逆过程。不同的实体集通过共同的属性提取为父集实体集。
Attribute Inheritance
Specialization 和 Generalization 中的高层的实体集被底层实体集继承。
Aggregation
E-R 模型中无法表示关系之间的关系。Aggregation 是一个把关系集作为更高层级的实体集的抽象。一个例子如下图所示:
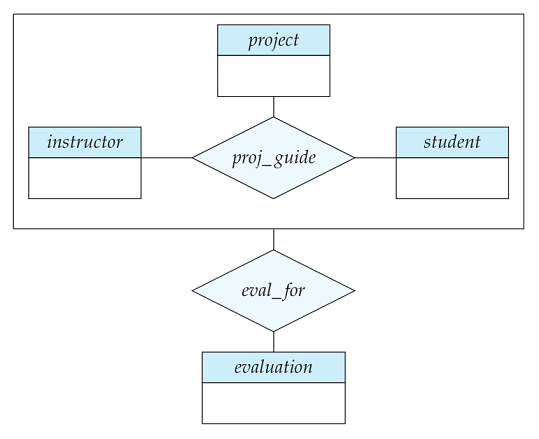
Extended E-R Features Reduction to Relation Schemas
E-R 模型扩展特性 Generalization 如何在关系型 Schema 中表示
第一种方式是,为更高层的实体集创建一个 schema,为每一个低层的实体集创建一个 schema,低层的 schema 属性由它特有的属性和高层的主键组成,添加一个外键约束,底层的 schema 主键参考高层 schema 的主键。如一个高层实体集下的两个低层实体集的关系型 schema 的例子:
person(ID, name, street, city) |
第二种方式是,当实体集只有两层,而且分化是完全的。可以不创建高层的 schema,只是创建第二层的 schema,底层的 schema 的属性由高层的属性和自己特有的属性组成。如下:
employee(ID, name, street, city, salary) |
上面两种方式都是用高层的实体集的主键作为它们自己的主键。第二种方式的缺点是:1)没有创建高层的实体集的 schema,当一个关系集与高层实体集关联时,无法参考这个实体集。避免这个问题可以创建一个 person 表,只包含它的主键。2)如果是 overlapping generalization 即一个实体可以同时作为多个子对象,那么一些值会重复的存储在多个表中。3)如果 disjoint 是不完整的,如有的对象不属于任何一个子对象,那么第二种方式无法表示这个对象。
E-R 模型扩展特性 Aggregation 如何在关系型 Schema 中表示
把 aggregation 当作一个实体集。aggregation 的主键就是关系集的主键。
其它的数据建模方式
E-R 图没有统一的标准,不同的地方可能使用不同的标识或图形。E-R 图可以帮助我们对系统组件的数据表现进行建模,但是数据表现只有系统设计的一部分,系统设计还需要设计,如用户和系统的交互,系统的功能模块的规范等等。我们可以使用 UML (Unified Modeling Language)来表示系统的更多的设计。
数据库设计的其它方面
Schema 的设计只是数据库设计中的一部分。其它方面的设计也不可忽略。
- 数据约束和关系型数据库设计。除了属性和关系,还是大量的数据约束需要设计,如主键约束,外键约束,检查约束,断言,和触发器等等。
- 使用需求。性能要求,如吞吐量(Throughput),响应时间(Response Time)。
- 数据库授权。
- 数据流工作流。
- 考虑未来可能的变化。
关系型数据库设计和标准化
关系型数据库设计的目标是生成一组关系 schema 使得存储信息没有不必要的冗余,以及高效地取出信息。实现这个目标可以通过设计一个满足范式(Normal Form)的 schema。
我们将介绍一种基于函数依赖(Functional Dependencies)的正式的关系数据库设计方法。 然后,我们根据函数依赖和其他类型的数据依赖定义范式。
好的关系型设计的特点
一个好的关系型数据库设计。
- 不能出现太多的数据冗余,需要将冗余的信息属性进行适当的分解。
- 不能过度的分解,使得丢失信息完整性。
关系型数据库设计的核心在于:在保证数据完整性的情况下,如何减少数据的冗余。以及如何在性能和冗余之间权衡。
Functional Dependencies
在介绍范式之前,我们需要先了解什么是函数依赖(functional dependencies)。
Notations
- 使用 Greek Letters 表示 Functional Dependency 中的一组属性。如 α, β。
- 使用小写 Roman Letter 加上在小括号中的大写 Roman Ltter 表示一个 relation schema,如 r(R),其中大写字母 R 表示一组属性。Greek Letter 表示的一组属性可能是部分属性或者全部属性,Roman Letter 一般表示全部属性。
- 一组属性组成的 superkey 使用 K 表示。我们可以说 K 是 r(R) 的一个 superkey。
- 我们使用小写表示关系。如 instructor。在定义或者算法中,使用单个字符表示关系,如 r 。
Functional Dependencies
表示一个 functional dependency 存在一个 schema 中的定义如下:
设 schema 为 r(R), α ⊆ R 且 β ⊆ R.
- 给定的一个 r(R) 的实例中,如果实例中的所有的元组对 t1 和 t2 满足:若 t1[α] = t2[α], 那么 t1[β] = t2[β],则可以说这个实例满足 functional dependency α ⟶ β。
- 如果在schema r(R) 的每一个合法的实例中,都满足一个 functional dependency α ⟶ β,则可以说这个 functional dependency α ⟶ β holds on schema r(R)。
使用 functional-dependency notation 表示一个 schema 的 superkey:如果 functional dependency K ⟶ R holds on r(R),则 K 是 r(R) 的一个 superkey。
具体的例子:使用 functional dependency 表示 inst_dept(ID, name, salary, dept_name, building, budge) 的 superkey:
ID, dept_name ⟶ name, salary, building, budget |
Functional Dependencies 有两种用途:
- 测试给定的 relation 的一个实例是否满足一组给定的 functional dependencies F。
- 指定对合法的 relation 的约束。
Trivial
一些 functional dependencies 是 trivial,因为它们满足所有的 relations。例如 A ⟶ A,AB ⟶ A。
Trivial functional dependencies 的定义:如果 β ⊆ α,则 functional dependencies α ⟶ β 是 trivial。
Closure
所有可以从给定的 functional dependencies F 推导出来的 functional dependencies 集合称为 closure of F,表示为 F+。F+ 包含了所有 F 中的 functional dependencies。
Logically Implied
我们可以证明有其他的 functional dependencies 也 hold on the schema,我们可以说这些 functional dependencies 是 logically Implied by F。更正式地说,给定一个 schema r(R),如果满足 F 每一个 r(R) 的实例也满足 ⨍,则一个 functional dependency ⨍ 是通过一组 functional dependencies F 逻辑暗示的(logically implied)。
如给定一个 relation schema r (A, B, C, G, H, I) 和一组 functional dependencies:A ⟶ B, A ⟶ C, CG ⟶ H, CG ⟶ I, B ⟶ H。那么 A ⟶ H 是 logically Implied。
closure of F 即 F+ 是一组所有被 F logically implied 的 functional dependencies。
Axioms
通过一些公理(Axioms)可以找到一个relation schema 的 logically implied functional dependencies。Armstrong‘s Axioms 表示如下:
- Relexivity rule。If α is a set of attributes and β ⊆ α, then α → β holds.
- Augmentation rule。 If α → β holds and γ is a set of attributes, then γα → γβ holds.
- Transitivity rule。 If α → β holds and β → γ holds, then α → γ holds.
Armstrong’s Axioms ,它是 sound,因为它们不生成任何不正确的 functional dependencies。它是 complete,因为对于给定的一组 functional dependencies F 它可以生成所有的 F+。
其它的公理:
- Union rule。 If α → β holds and α → γ holds, then α → βγ holds.
- Decomposition rule。If α → βγ holds, then α → β holds and α → γ holds.
- Pseudotransitivity rule。 If α → β holds and γβ → δ holds, then αγ → δ holds.
Formal Forms
常见的范式(Formal Forms)有:第一范式,第二范式,第三范式,BC 范式,和第四范式。
Atomic Domains and First Normal Form
为了减少单个属性的数据冗余,我们常用的方法是:对于组合属性,如 address 由 street,city,state 和 zip 等组成,我们创建一个单独的表来表示这些属性。对于多值属性,我们让每一个多值属性中的每一项作为一个单独的属性。
在关系模型中,我们通过形式化(Formalize)来实现一个属性没有任何子结构。如果一个 domain 是不可再分的单元称这个 domain is atomic。我们定义:如果一个 relation schema R 中的所有属性的 domain 是 atomic,则称这个 schema R 是在 First Normal Form (1NF,第一范式) 中的。
Boyce-Codd Normal Form
Boyce-Codd Normal Form (BCNF) 它消除了可以基于 functional dependencies 发现的所有数据冗余。但是可能存在一些其它类型的的冗余,需要用其它的方法来解决,如 multivalue dependencies。
如果对于来自 α → β, a ⊆ R, β ⊆ R 的 F+ 中的所有 functional dependencies 满足以下至少一项条件,则 relation schema R 的 functional dependencies F 在BCNF中:
- α → β 是一个 trivial functional dependency。
- α 是 schema R 的一个 superkey。
以上条件可以理解为:schema 中的任何 nontrivial functional dependency 的左侧必须是一个 superkey。
一个 schema 不在 BCNF 中的例子:
inst_dept (ID, name, salary, dept_name, building, budget) |
其中存在 dept_name → budget hold on inst_dept,由于它不是一个 trivial functional dependency,且 dept_name 不是一个 superkey。BCNF 的两个可选项一个也不满足,所以 inst_dept 不在 BCNF 中。
一个不在 BCNF 中的 schema 可以进行分解。分解为两个 schema 如下:
- (α ∩ β)
- (R - (β - α))
注意其中 “-” 表示属性集之间的差集。
如 inst_dept (ID, name, salary, dept_name, building, budget) 中 α = dept_name, β = {building, budget}, α → β 不满足 BCNF,inst_dept 分解为:
- (α ∩ β) = (dept_name, building, budget)
- (R - (β - α)) = (ID, name, dept_name, salary)
Third Normal Form
Third Normal Form(3NF,第三范式)通过允许某些 nontrivial functional dependencies (其左侧不是 superkey)来稍微放松约束。
如果对于来自 α → β, 其中 a ⊆ R, β ⊆ R 的 F+ 中的所有 functional dependencies 满足以下至少一项条件,则 relation schema R 的 functional dependencies F 在 3NF 中:
- α → β 是一个 trivial functional dependency。
- α 是 schema R 的一个 superkey。
- β - α 中的每一个属性 A 是包含于 R 的 candidate key 中的。
3NF 的定义前两个可选项是和 BCNF 一样的,它多给出了一个可选项。任何满足 BCNF 的 schema 也满足 3NF,BCNF 是更严格的 3NF。
如,schema dept_advisor(s_ID, i_ID, dept_name),存在下面的 functional dependencies:
i_ID → dept_name |
可以看出 i_ID → dept_name 不在 BCNF 中。α = i_ID, β = dept_name, β - α = dept_name,因为 s_ID, dept_name → i_ID hold on dept_advisor,dpet_name 包含于 candidate key中,所以 dept_advisor 是在 3NF 中的。
Multivalue Dependencies and Fourth Normal Form
从某种意义上说,一些 relation schema 即使它们在 BCNF 中,似乎仍未得到足够的规范化(normalized),因为它们仍然遭受信息重复的问题。Multivalue dependencies 就是这一类的数据冗余问题,而 Fourth Normal Form (4NF,第四范式)就是为了消除 multivalue dependencies 问题。
Multivalue Dependencies(多值依赖)使用双箭头 “↠” 符号表示,如 A ↠ B。如果一个关系同时满足下面三个条件,则这个relation schema 存在 multivalue dependencies:
- 一个属性 A 的值,对应多个属性 B 的值。
- 关系表至少由 3 个属性。
- 设关系表有三个属性分别为 A,B,C,属性 B 和 C 是独立的。
如下列 enrolment 表存在多值依赖 s_id ↠ hobby。其中,s_id 表示学生ID,course 表示课程,hobby 表示爱好。
| s_id | course | hobby |
|---|---|---|
| 1 | science | Cricket |
| 1 | math | Hockey |
| 1 | science | Hockey |
| 1 | math | Cricket |
消除多值依赖,将它分解为两个表。
stu_course
| s_id | cource |
|---|---|
| 1 | science |
| 1 | math |
stu_hobby
| s_id | hobby |
|---|---|
| 1 | Hockey |
| 1 | Cricket |
Second Normal Form
一个 schema 在 Second Normal Form (2NF,第二范式)它需要满足以下条件:
- 它是在 1NF 中的。
- 所有非键属性是完全 functional dependent on the primary key。
如下 purchase_detail schema:
purchase_detail(customerID, storeID, purchase_location) |
它的主键是 customerID 和 storeID。但存在 functional dependency storeID → purchase_location,storeID 不是完整的 primary key 所以 purchase_detail 不在 2NF 中。我们将 purchase_detail 进行分解使他满足 2NF:
purchase(customerID, storeID) |
范式总结
| 名称 | 定义 | |
|---|---|---|
| 1NF | 单个属性原子性,不可再分 | |
| 2NF | 1. 满足 1NF 。2. 没有部分依赖。非键属性完全依赖于主键属性。 | |
| 3NF | 1. 满足 2NF 。2. 没有传递依赖。每一个非 nontrivial functional dependency X → Y, X 是一个 superkey,或者 Y 是 prime attributes(part of candidate key)。 | |
| BCNF | 1. 满足 3NF。2. 每一个非 nontrivial functional dependency X → Y, X 是一个 superkey。 | |
| 4NF | 1. 满足 BCNF。2. 没有 multivalue dependencies。 |
小结
E-R 模型专注于实体和它们之间的关系,而标准化专注于去除冗余数据,防止数据修改不完整,标准化有利于保证数据的一致性。完整性约束防止数据错误修改,与标准化类似,它也是为了保证数据的一致性。
深入理解数据库系统系列文章
References
[1] Database System Concept (6th) by Avi Silberschatz, Henry F. Korth, and S. Sudarshan